Graphics

Research

3D Vectorization

As my primary research project in the Geometry Collective, I have been working on a pipeline for 3D vectorization. 3D vectorization is the process of rendering a 3D scene to vector graphics, such as SVG. Currently, my advisor, professor Keenan Crane, and I are working on a submission of the project to SIGGRAPH.

For our method, we compute a wireframe rendering of the 3D scene, generating a series of 2D curves that represent the edges and silhouettes of the 3D geometry. We then compute a planar arrangment of our curves, which gives the set of disjoint planar regions formed by our silhouette curves. This planar arrangment includes curves occluded by other geometry, so finally we simplify the planar arrangment by removing occluded curves. This final planar arrangment gives the occluded vector output, which can be saved into common vector graphics formats (i.e. SVG).

The crux of the problem, and the main contribution of our research, is in computing the arrangment of these curves. Existing methods, primarily based on the Bentley-Ottmann sweepline algorithm, are often plagued by numerical issues. These numerical issues are fixed by using arbitrary-precision floating point numbers, which are inefficient.

By contrast, our method computes the arrangment of curves by building a BSP tree over the set of curves. By using a BSP tree method, we can guarantee the validity of our output without resorting to arbitrary-precision numbers. This allows us to vectorize 3D scenes with both numerical robustness and efficiency.

Below is an example output from our pipeline, rendered in SVG format.

Course Projects

Vulkan Renderer

As a part of the Real-Time Computer Graphics course at CMU, I wrote a full rendering engine completely from scratch using C++ and Vulkan. The renderer supports frustum culling, PBR materials, normal and parallax occlusion mapping, pre-filtered environment maps, real-time point/spot/sun lights, and shadow mapping. Additionally, for the final project of the course, I implemented parallax-corrected environment maps as described by Sebastian Lagarde in a SIGGRAPH 2012 talk. The source code can be found on my Github.

Specular Next Event Estimation

For the final project of the Phyiscally-Based Rendering course at CMU, I implemented the paper Slope-Space Integrals for Specular Next Event Estimation by Loubet et. al. The method was implemented on top of a standard path tracer.

In order to perform specular next event estimation as described in the paper, we define a method for computing the specular contribution of a triangle by integrating in slope-space. We can then importance sample a point on the triangle by using Newton’s method to inversion sample the specular contribution. In order to eliminate triangles with low specular contribution during importance sampling, we precompute a specular BVH, which bounds which regions have a high specular contribution from a given triangle.

My implementation of the method was one of two projects which won the technical award for the class final project competition.

Hobby Projects

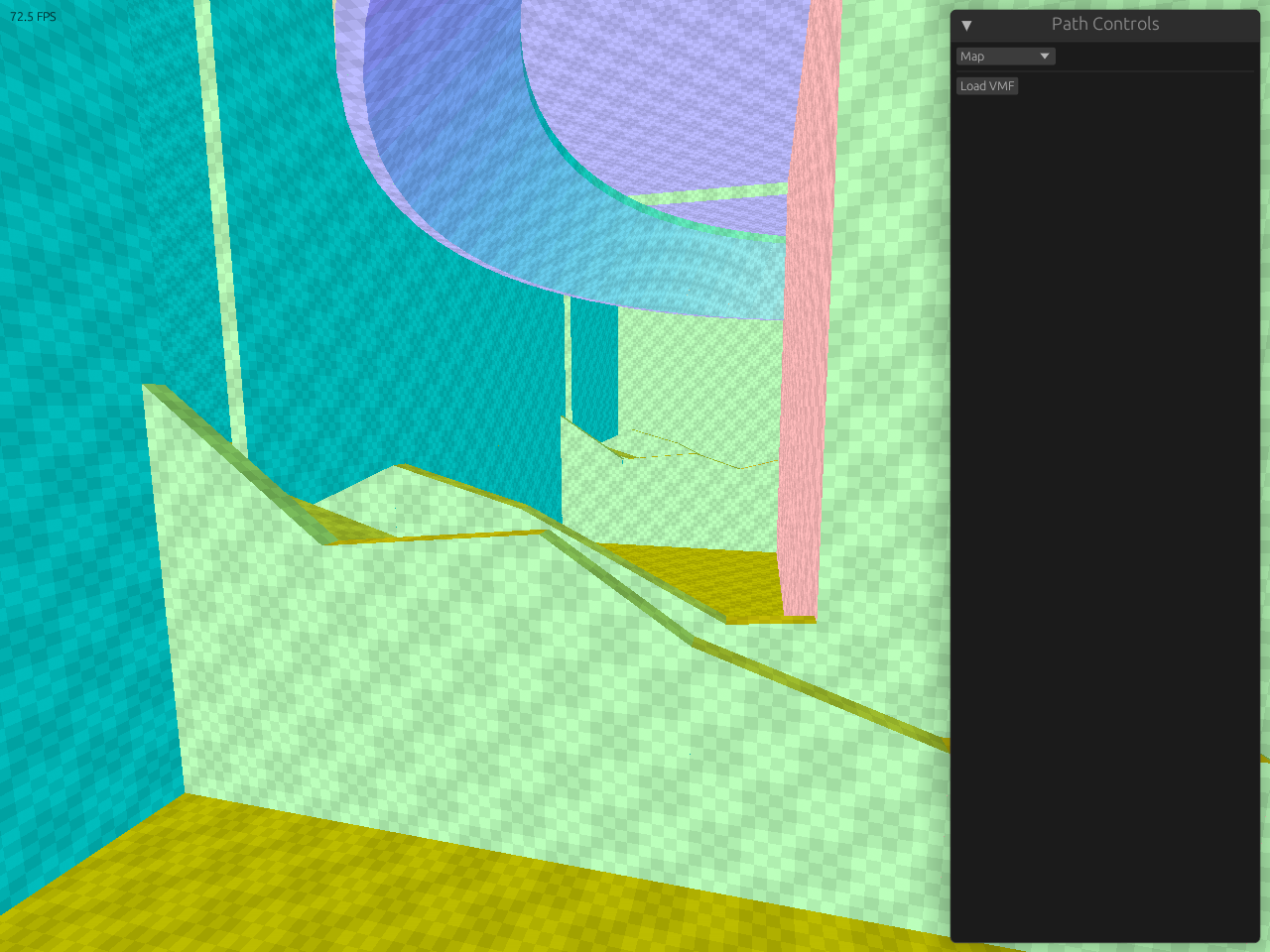
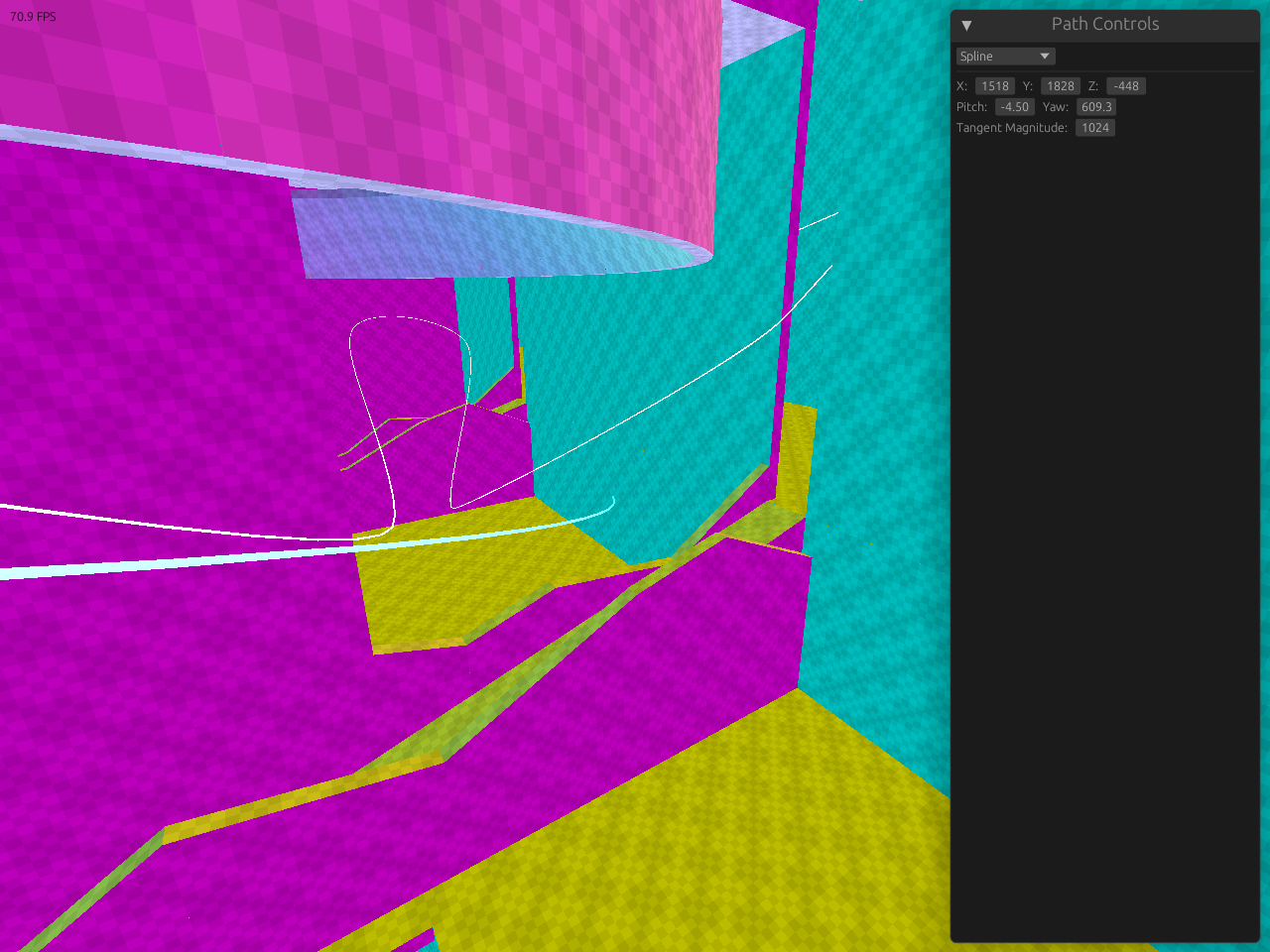
Spline Generator

As a part of my Counter Strike level design, I wanted to easily create 3D models of spline curves that weave through my levels. To help create these models, I wrote a tool that lets me freehand these splines easily, and then export them into a format that I could use in Counter Strike. The tool uses a custom engine, loading the Counter Strike map format to allow me to visualize how the splines look within the environment. I can easily add new points to my spline, as well as adjust the position and rotation of existing control points, all within the tool. The tool is written in Rust and uses WebGPU to render both on native and the web. The source code can be found here.